Merge Sort

Algorithm Analysis

The merge sort splits the list to be sorted into two equal halves, and places them in separate arrays. Each array is recursively sorted, and then merged back together to form the final sorted list. Like most recursive sorts, the merge sort has an algorithmic complexity of O(n log n).

Elementary implementations of the merge sort make use of three arrays - one for each half of the data set and one to store the sorted list in. The below algorithm merges the arrays in-place, so only two arrays are required. There are non-recursive versions of the merge sort, but they don't yield any significant performance enhancement over the recursive algorithm on most machines.

Pros: Marginally faster than the heap sort for larger sets.
Cons: At least twice the memory requirements of the other sorts; recursive.

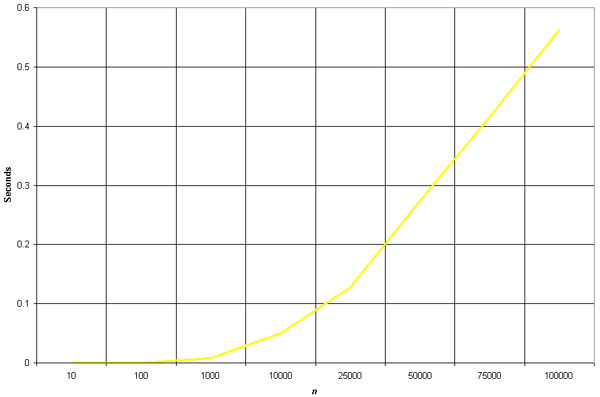
Empirical Analysis

Merge Sort Efficiency

The merge sort is slightly faster than the heap sort for larger sets, but it requires twice the memory of the heap sort because of the second array. This additional memory requirement makes it unattractive for most purposes - the quick sort is a better choice most of the time and the heap sort is a better choice for very large sets.

Like the quick sort, the merge sort is recursive which can make it a bad choice for applications that run on machines with limited memory.

Source Code
Below is the basic merge sort algorithm.

void mergeSort(int numbers[], int temp[], int array_size)
{
  m_sort(numbers, temp, 0, array_size - 1);
}


void m_sort(int numbers[], int temp[], int left, int right)
{
  int mid;

  if (right > left)
  {
    mid = (right + left) / 2;
    m_sort(numbers, temp, left, mid);
    m_sort(numbers, temp, mid+1, right);

    merge(numbers, temp, left, mid+1, right);
  }
}

void merge(int numbers[], int temp[], int left, int mid, int right)
{
  int i, left_end, num_elements, tmp_pos;

  left_end = mid - 1;
  tmp_pos = left;
  num_elements = right - left + 1;

  while ((left <= left_end) && (mid <= right))
  {
    if (numbers[left] <= numbers[mid])
    {
      temp[tmp_pos] = numbers[left];
      tmp_pos = tmp_pos + 1;
      left = left +1;
    }
    else
    {
      temp[tmp_pos] = numbers[mid];
      tmp_pos = tmp_pos + 1;
      mid = mid + 1;
    }
  }

  while (left <= left_end)
  {
    temp[tmp_pos] = numbers[left];
    left = left + 1;
    tmp_pos = tmp_pos + 1;
  }
  while (mid <= right)
  {
    temp[tmp_pos] = numbers[mid];
    mid = mid + 1;
    tmp_pos = tmp_pos + 1;
  }

  for (i=0; i <= num_elements; i++)
  {
    numbers[right] = temp[right];
    right = right - 1;
  }
}

A sample C program that demonstrates the use of the merge sort may be downloaded here.