Shell Sort

Algorithm Analysis

Invented by Donald Shell in 1959, the shell sort is the most efficient of the O(n²) class of sorting algorithms. Of course, the shell sort is also the most complex of the O(n²) algorithms.

The shell sort is a "diminishing increment sort", better known as a "comb sort" to the unwashed programming masses. The algorithm makes multiple passes through the list, and each time sorts a number of equally sized sets using the insertion sort. The size of the set to be sorted gets larger with each pass through the list, until the set consists of the entire list. (Note that as the size of the set increases, the number of sets to be sorted decreases.) This sets the insertion sort up for an almost-best case run each iteration with a complexity that approaches O(n).

The items contained in each set are not contiguous - rather, if there are i sets then a set is composed of every i-th element. For example, if there are 3 sets then the first set would contain the elements located at positions 1, 4, 7 and so on. The second set would contain the elements located at positions 2, 5, 8, and so on; while the third set would contain the items located at positions 3, 6, 9, and so on.

The size of the sets used for each iteration has a major impact on the efficiency of the sort. Several Heroes Of Computer Science^TM, including Donald Knuth and Robert Sedgewick, have come up with more complicated versions of the shell sort that improve efficiency by carefully calculating the best sized sets to use for a given list.

Pros: Efficient for medium-size lists.
Cons: Somewhat complex algorithm, not nearly as efficient as the merge, heap, and quick sorts.

Empirical Analysis

Shell Sort Efficiency

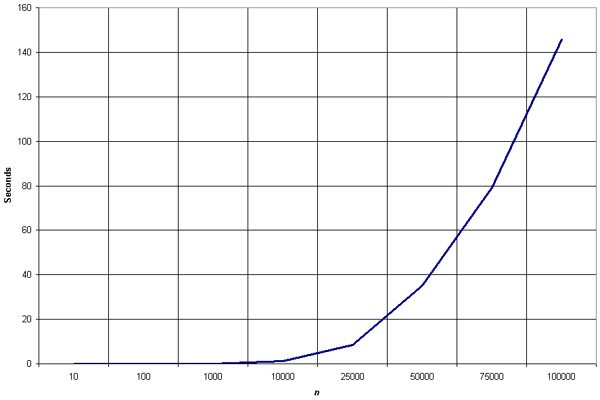
The shell sort is by far the fastest of the N² class of sorting algorithms. It's more than 5 times faster than the bubble sort and a little over twice as fast as the insertion sort, its closest competitor.

The shell sort is still significantly slower than the merge, heap, and quick sorts, but its relatively simple algorithm makes it a good choice for sorting lists of less than 5000 items unless speed is hyper-critical. It's also an excellent choice for repetitive sorting of smaller lists.

Source Code
Below is the basic shell sort algorithm.

void shellSort(int numbers[], int array_size)
{
  int i, j, increment, temp;

  increment = 3;
  while (increment > 0)
  {
    for (i=0; i < array_size; i++)
    {
      j = i;
      temp = numbers[i];
      while ((j >= increment) && (numbers[j-increment] > temp))
      {
        numbers[j] = numbers[j - increment];
        j = j - increment;
      }
      numbers[j] = temp;
    }
    if (increment/2 != 0)
      increment = increment/2;
    else if (increment == 1)
      increment = 0;
    else
      increment = 1;
  }
}

A sample C program that demonstrates the use of the shell sort may be downloaded here.