

|
EIDORS: Electrical Impedance Tomography and Diffuse Optical Tomography Reconstruction Software |
|
EIDORS
(mirror) Main Documentation Tutorials − Image Reconst − Data Structures − Applications − FEM Modelling − GREIT − Old tutorials − Workshop Download Contrib Data GREIT Browse Docs Browse SVN News Mailing list (archive) FAQ Developer
|
GREIT Reconstruction MatrixThe AUSPEX Software is an EIT evaluate and analysis software from Carefusion. AUSPEX is designed to analyse data collected from the Geo II MF EIT system. It uses a reconstruction algorithm based on Sheffield backprojection.To replace this algorithm with GREIT algorithm, one needs to replace the file ReconstructionMatrixF.mat with another one calculated by this tutorial. Circular GREIT model
n_elecs = 16;
fmdl = ng_mk_cyl_models([1 1 0.1] ,[n_elecs,.5],[0.05]);
% NOTE: The 'rotate_meas' is essential here.
fmdl.stimulation = mk_stim_patterns(n_elecs,1,[0,1],[0,1],{'rotate_meas','no_meas_current'}, 1);
fmdl = mdl_normalize(fmdl, 1); %MUST FOR AUSPEX
opt.imgsz = [32 32];
opt.distr = 3;
opt.noise_figure = 0.5;
imdl = mk_GREIT_model(fmdl, 0.20, [], opt);
% DESTINATION AUSPEX MODEL
cmdl = mk_common_gridmdl('b2d','backproj');
cmdl = rmfield(cmdl.fwd_model,'coarse2fine');
% MODEL GEOMETRIES MUST MATCH
f2c = mk_coarse_fine_mapping(cmdl, imdl.rec_model);
RM = f2c*imdl.solve_use_matrix.RM(1:size(f2c,2),:);
ReconstrMatrix= - ( RM(1:2:end,:) + RM(2:2:end,:) )';
save ReconstrMatrixGREITc ReconstrMatrix -V6;
Adult human GREIT model
n_elecs = 16;
fmdl= mk_library_model('adult_male_16el');
fmdl.electrode = fmdl.electrode([9:16,1:8]);
fmdl.electrode = fmdl.electrode([1,16:-1:2]);
fmdl.stimulation = mk_stim_patterns(n_elecs,1,[0,1],[0,1],{'rotate_meas','no_meas_current'}, 1);
fmdl = mdl_normalize(fmdl, 1);
img = mk_image(fmdl,1); % Homogeneous background
opt.imgsz = [32 32];
opt.distr = 3;
opt.noise_figure = 0.5;
imdl = mk_GREIT_model(fmdl, 0.25, [], opt);
% MODEL
fmdl = imdl.rec_model;
fmdl.nodes = fmdl.nodes/max(fmdl.nodes(:))*1.1*[1,0;0,-1];
cmdl = mk_common_gridmdl('b2d','backproj');
cmdl = rmfield(cmdl.fwd_model,'coarse2fine');
f2c = mk_coarse_fine_mapping(cmdl, fmdl);
RM = f2c*imdl.solve_use_matrix.RM(1:size(f2c,2),:);
ReconstrMatrix= - ( RM(1:2:end,:) + RM(2:2:end,:) )';
save ReconstrMatrixGREITt ReconstrMatrix -V6;
Test Simulations
imdl = mk_common_model('c2c2',16);
imdl.fwd_model.stimulation = ...
mk_stim_patterns(16,1,[0,1],[0,1],{'rotate_meas','no_meas_current'},1);
img = mk_image(imdl); vh = fwd_solve( img );
img.elem_data(290) = 1.1; vi = fwd_solve( img );
clf;subplot(221);
show_fem(img); title('Test Object');
print_convert GREIT_AUSPEX03a.png
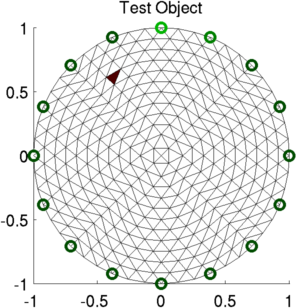
Figure: Simulation with target to test AUSPEX matrix Test of GREIT/AUSPEX matrices
s=1;
fnames = {'ReconstrMatrixGREITc.mat','ReconstrMatrixGREITt.mat'};
for i=1:length(fnames);
load(fnames{i});
imdl = mk_common_gridmdl('b2d',ReconstrMatrix');
imgr= inv_solve(imdl, vh, vi);
subplot(2,2,s+0); show_fem(imgr);
title('Test Object Reconstruction');
imgr.elem_data = mean(ReconstrMatrix==0)';
subplot(2,2,s+1); show_fem(imgr);
title('Domain Boundary');
s=s+2;end
print_convert GREIT_AUSPEX04a.png

Figure: LeftReconstructions. RightReconstruction Domain |
Last Modified: $Date: 2017-02-28 13:12:08 -0500 (Tue, 28 Feb 2017) $ by $Author: aadler $